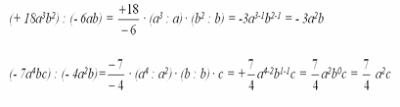La moltiplicazione fra due o più monomi può essere indicata in diversi modi:

(+3ab²) ^. (-4a²b)

(+3ab²)   (-4a²b)

+3ab²(-4a²b)

Vediamo ora di calcolare l’esempio sopra

(+3ab²) ^. (-4a²b) = - 12 a¹⁺² b²⁺¹ =  - 12 a³b³

La regola da ricordare è che il prodotto di due monomi è un monomio che ha come coefficiente il prodotto dei coefficienti e la parte letterale composta da tutte le lettere che compaiono nei monomi, considerate una sola volta e con esponente uguale alla somma degli esponenti che la lettera stessa ha nei monomi.

Vediamo un altro esempio 

Proviamo ora ad eseguire una divisione fra monomi. 

La regola da ricordare è che il quoziente tra due monomi è un monomio che ha come coefficiente il quoziente dei coefficienti e la parte letterale composta da tutte le lettere che compaiono nel dividendo, con esponente uguale alla differenza degli esponenti con cui la lettera stessa compare nel dividendo e nel divisore.

Ecco un altro esempio 

Consideriamo ora come calcolare la potenza di un monomio. 

Vediamo che praticamente per calcolare la potenza n di un monomio dobbiamo scrivere un monomio calcolando la potenza n del coefficiente e indicando la parte letterale formata da tutte le lettere aventi per esponente il prodotto del proprio esponente per n.

Un altro esempio. 

ESERCIZI

·     Esegui le seguenti moltiplicazioni tra monomi 

·     Esegui le seguenti divisioni tra monomi 

·        Calcola le potenze dei seguenti monomi