Sappiamo già che possiamo considerare la frazione come operatore, in quanto ci permette di operare su di una grandezza.

Ora consideriamo invece la frazione come quoziente tra due numeri, il numeratore ed il denominatore.

2/5 = 2 : 5

Consideriamo per un momento i numeri naturali e scopriremo che qualunque numero naturale si può scrivere sotto forma di frazione.

Cominciamo dallo “0”: si può scrivere come una frazione avente “0” al numeratore. Infatti:

0/4 = 0 : 4 = 0

0/6 = 0 : 6 = 0

Passiamo al numero 1: si può indicare con una frazione apparente con numeratore uguale al denominatore

3/3 = 3 : 3 = 1

5/5 = 5 : 5 = 1

Tutti gli altri numeri naturali si possono scrivere con una frazione con denominatore 1

10/1 = 10 : 1 = 10

7/1 = 7 : 1 = 7

oppure

con una frazione avente al numeratore un multiplo del denominatore. Ad esempio se io volessi scrivere il numero 15 sotto forma di frazione potrei scrivere così: 15/1, 30/2, 45/3, ecc

Considerando la frazione come quoziente tra due numeri, possiamo quindi stabilire un nuovo insieme che includerà tutte le frazioni. Chiameremo questo insieme come insieme Q⁺. 

Da quanto detto sopra possiamo facilmente capire come l’insieme dei numeri naturali N sia un sottoinsieme dell’insieme Q⁺ ed indicheremo questa relazione così: N Ì Q⁺.

Sappiamo già che le frazioni godono della proprietà invariantiva: moltiplicando o dividendo sia il numeratore che il denominatore per uno stesso numero, si ottiene una frazione equivalente a quella data.

Consideriamo ad esempio la frazione ¾. Alcune frazioni equivalenti sono 6/8, 9/12, 12/16, 15/20, ecc.

E’ evidente che le frazioni equivalenti ad una data sono infinite.

Tutte le frazioni equivalenti ad una frazione data appartengono ad una classe di equivalenza. Se consideriamo, ad esempio, la frazione 3/5 avremo la classe di equivalenza:

A = {3/5, 6/10, 9/15, 12/20, 15/25, 18/30, ………}

Consideriamo la classe di equivalenza sopra descritta: se calcoliamo il valore numerico di frazioni che appartengono ad una stessa classe di equivalenza ci accorgiamo che il risultato è sempre uguale.

3/5 = 3 : 5 = 0,6

6/10 = 6 : 10 = 0,6

9/15 = 9 : 15 = 0,6

12/20 = 12 : 20 = 0,6

Possiamo allora rappresentare tutta la classe con una sola frazione della classe, quella irriducibile.

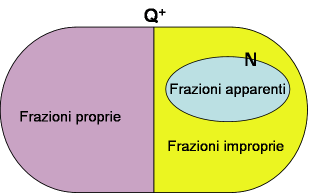
L’insieme di tutte le classi di equivalenza è l’insieme Q⁺ che viene chiamato insieme dei numeri razionali, che, come abbiamo visto include anche l’insieme N dei numeri naturali. Possiamo sintetizzare con il diagramma di Eulero Venn

Proviamo ora a rappresentare i numeri naturali su una semiretta orientata

Immaginiamo di voler rappresentare il numero razionale {1/3; 2/6; 3/9; 4/12; …..}

Consideriamo la frazione che rappresenta la classe di equivalenza 1/3 ed operiamo dividendo l’unità di misura in 3 parti e considerandone 1. Il punto T è l’immagine del numero razionale {1/3; 2/6; 3/9; 4/12; …..} mentre il punto T’ è l’immagine del numero razionale {8/3; 16/6; 24/9; 32/12; …..}

Vediamo un altro esempio

ESERCIZI

·    L’insieme dei numeri razionali forma un nuovo insieme numerico, detto ……………………………

·    L’insieme N dei numeri naturali è un sottoinsieme di questo nuovo insieme?

·    In quale modo la frazione 4/5 può essere considerata come il quoziente tra due numeri?

·    Prova a scrivere sotto forma di frazioni i numeri:

     2, 7, 15, 19

·    Individua il numero razionale rappresentato dalla frazione 2/5. Esso è minore, maggiore o uguale ad 1?

·    Individua il numero razionale rappresentato dalla frazione 5/4. Esso è minore, maggiore o uguale ad 1?

·    Individua il numero razionale rappresentato dalla frazione 3/1. Il numero che hai scritto è uguale a quale numero naturale?

·    Scrivi alcuni numeri razionali rappresentati dalle seguenti frazioni

5/8 = {……………………..………}

7/5 = {……………………..………}

2/3 = {……………………..………}

7/1 = {……………………..………}