La Congruenza, la traslazione e la rotazione
In geometria si chiamano movimenti rigidi le trasformazioni che non alterano la forma e l’estensione di una figura.
Due figure geometriche sono congruenti quando, in seguito ad una sovrapposizione attuata con uno o più movimenti rigidi che non comportino deformazioni, coincidono perfettamente.
Per controllare se due figure sono congruenti dobbiamo procedere ad una sovrapposizione attuando un movimento rigido.
Possiamo avere due tipi di movimenti: diretti od inversi.
Consideriamo questo esempio:
Per sovrapporre queste due figure è sufficiente spostare la prima sul piano finché i suoi vertici coincidono con la seconda figura: si tratta di un
movimento diretto che avviene nel piano in cui giacciono le due figure. Le due figure si dicono direttamente congruenti.
Se invece consideriamo quest’altro esempio:
vediamo che per sovrapporre le due figure bisogna prima operare un ribaltamento di A, uscendo quindi dal piano in cui giacciono le figure, e successivamente uno spostamento per sovrapporre i
vertici: si tratta di un movimento inverso che si compie uscendo dal piano che contiene le due figure da sovrapporre. Le due figure si dicono inversamente congruenti.
La relazione di congruenza si indica con il simbolo @.
Quindi possiamo dire che A @ A’
La relazione di congruenza gode della proprietà riflessiva: ogni figura è congruente a se stessa.
A @ A
La relazione di congruenza gode della proprietà simmetrica: se A è congruente ad A’, anche A’ sarà congruente ad A.
Se A @ A’Þ A’ @ A
La relazione di congruenza gode della proprietà transitiva: se la figura A è congruente alla figura B e la figura B è congruente alla figura C allora anche A sarà congruente a C.
Se A @ B e B @ C Þ A @ C
Poiché la relazione di congruenza gode delle proprietà riflessiva, simmetrica e transitiva, possiamo dire che la relazione di congruenza è una relazione di equivalenza.
ESERCIZI
· Quali, tra
le seguenti affermazioni, sono vere?
o La relazione
di congruenza è una relazione di equivalenza
o La congruenza
mantiene uguale l’ampiezza degli angoli, ma non la lunghezza dei segmenti
o Due figure
sono congruenti se coincide un solo vertice
o La relazione
di congruenza è una relazione che non altera la forma e l’estensione di una figura
· Di quali
proprietà gode la relazione di congruenza?
· Qual è la
proprietà indicata in simboli?
A @ A
Se A @ B e B @ C Þ A @ C
Se A @ A’Þ A’ @ A
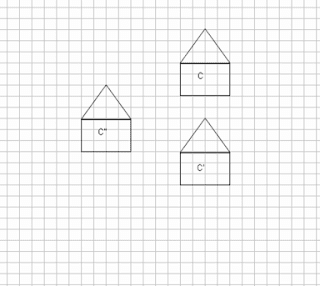
· Indica con
quale movimento si passa da una figura alle successive figure congruenti
Da A ad A’: movimento …………………
Da A’ ad A’’: movimento …………………
Da A ad A’’: movimento …………………
· Indica con
quale movimento si passa da una figura alle successive figure congruenti
Da B ad B’: movimento …………………
Da B’ ad B’’: movimento …………………
Da B ad B’’: movimento …………………
· Disegna la
figura congruente che si ottiene con un movimento diretto
· Disegna la
figura congruente che si ottiene con un movimento inverso
Dopo aver esaminato la congruenza, vediamo un altro movimento rigido, la traslazione.
Quella che vedi sopra è una traslazione.
Nel linguaggio matematico il termine “traslazione” significa un movimento rigido di un corpo (che, quindi, non altera né la forma né l’estensione) in cui le
traiettorie descritte da ciascuno dei punti che lo compongono sono uguali e parallele.
Puoi verificare nella figura sopra che le linee tratteggiate che descrivono lo spostamento dei punti al vertice risultano essere tra loro parallele e della stessa lunghezza.
Per individuare una traslazione occorre sapere la lunghezza (o modulo), la direzione ed il verso della stessa.
A tal fine si usa il vettore, cioè un segmento con una lunghezza definita (detta anche modulo), una direzione data dalla retta a cui appartiene ed
un versoindicato dalla punta della freccia.
Ecco, ad esempio, il vettore della traslazione raffigurata sopra.
E’ evidente che due figure ottenute per traslazione sono direttamente congruenti.
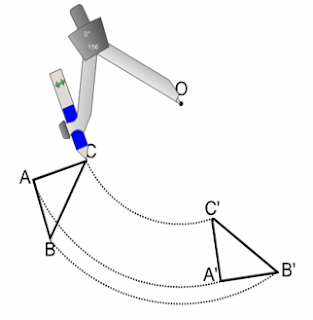
Un altro movimento rigido è la rotazione.
Immaginiamo di avere un punto A qualsiasi e di sottoporlo ad una rotazione.
Ci serve un punto fisso, che chiameremo O, sul quale puntiamo il compasso che avrà un’apertura uguale alla lunghezza del segmento OA
Per sapere quale dovrà essere l’ampiezza e il verso della rotazione ci serve un angolo orientato che ci indichi l’ampiezza (o modulo) ed il verso orario o antiorario. Immaginiamo
di voler ruotare il punto A secondo l’angolo orientato
Ricordiamo che l’angolo orientato si indica diversamente a seconda che il verso della rotazione sia orario o antiorario.
Riepilogando: abbiamo il compasso puntato in O con apertura uguale al segmento OA, ruotiamo il compasso in verso orario descrivendo un arco di 50°. Il punto A’ all’estremità dell’arco è il
corrispondente di A.
Nel linguaggio matematico il termine “rotazione” indica un movimento rigido di un corpo (che, quindi, non altera né la forma né l’estensione) individuato da un centro
di rotazione (il punto fisso O) e da un angolo orientato che indica l’ampiezza ed il verso di spostamento.
Proviamo ora ad effettuare una rotazione, individuata dal punto fisso O, di un triangolo ABC secondo l’angolo orientato
Sarà sufficiente effettuare la rotazione dei vertici A, B, C secondo la modalità già descritta in modo da trovare i corrispondenti A’, B’, C’.
ESERCIZI
· Come sono due figure ottenute per
traslazione?
· Che cos’è una rotazione?
· Come puoi spiegare il concetto di angolo
orientato?
· Disegna le figure A’ e A’’ ottenute (sempre
partendo da A) con le traslazioni individuate dai due vettori indicati.
· Disegna le figure B’, B’’, B’’’ ottenute con le traslazioni individuate dai tre vettori indicati, applicandole successivamente ad ogni figura ottenuta.
· Qual è il vettore che individua
la seguente traslazione?
· Quali sono i due vettori che
individuano le seguenti traslazioni successive?
· Data la figura disegnata,
effettua la rotazione di centro O e dell’ampiezza indicata