Sappiamo che ogni poligono regolare può essere diviso in tanti triangoli congruenti quanti sono i lati del poligono (un pentagono in 5 triangoli, un esagono in 6 e così via).

La base di ognuno di questi triangoli coincide con il lato del poligono mentre l’altezza è detta  apotema (a).

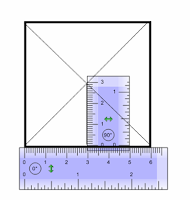
Consideriamo un poligono regolare, ad esempio un quadrato, con il lato di 4 cm e misuriamo la sua apotema. Otteniamo a = 2 cm. Dividiamo la misura dell’apotema per il lato 2 : 4 = 0,5

Vediamo poi che un quadrato con il lato di 5 cm ha l’apotema lunga 2,5 cm. Dividiamo la misura dell’apotema per il lato 2,5: 5 = 0,5

Vediamo anche un quadrato con il lato di 6 cm ha l’apotema lunga 3 cm. Dividiamo la misura dell’apotema per il lato 3 : 6 = 0,5

C’è un rapporto costante tra la misura dell’apotema e quella del lato del quadrato.  Provando anche con altri poligoni regolari constateremo sempre un rapporto costante (dipendente dal numero dei lati del poligono) tra la misura dell’apotema e quella del lato. Possiamo indicare questa costante con f.

Ecco le costanti di alcuni poligoni regolari, arrotondate a tre cifre decimali (quella del quadrato è esatta):

Di conseguenza, conoscendo la misura del lato del poligono si può calcolare anche l’apotema:

a = l x f

Conoscendo l’apotema si può calcolare la misura del lato

l = a/f

Vediamo ora come si può calcolare l’area di un poligono regolare.

Ricordando che un poligono regolare di n lati si può scomporre in n triangoli congruenti, per calcolare l’area sarà sufficiente calcolare l’area di uno dei triangoli e moltiplicare il risultato per n (nel pentagono regolare l’area di un triangolo x 5, nell’esagono regolare l’area di un triangolo per 6, ecc.). Vediamo un esempio con l’ettagono regolare:

Constatiamo come 7 x l corrisponda al perimetro dell’ettagono, quindi la formula può diventare valida per ogni poligono regolare:

da cui possiamo ricavare le formule inverse

p = A x 2/a

a = A x 2/p

ESERCIZI

·        Completa la seguente tabella

·        Un pentagono regolare ha l’apotema di 3,784 m. Calcola la sua area.

·        Un esagono regolare ha il perimetro di 49,2 dm. Quanto misura la sua superficie?

·        Un ettagono regolare ha l’area di 59,64 m² e l’apotema misura 4,26 m. Calcola la misura di un suo lato.

·        Un ottagono regolare ha il lato di 50 cm. Calcola l’altezza di un rettangolo equivalente all’ottagono ed avente la base di 142 cm.