Consideriamo alcune caratteristiche del triangolo isoscele:

·      Gli angoli alla base sono congruenti

·      L’altezza, l’asse, la mediana e la bisettrice relativi alla base coincidono in un unico segmento

·      Ortocentro (O), circocentro (C), baricentro (B) ed incentro (I) sono punti che si trovano su questo unico segmento.

 Vediamo ora le caratteristiche del triangolo equilatero:

·      Ha i tre lati congruenti e gli angoli stessa ampiezza (60°): è quindi un poligono regolare

·      L’altezza, l’asse, la mediana e la bisettrice relativi ad un qualunque lato coincidono in un unico segmento

·      Ortocentro (O), circocentro (C), baricentro (B) ed incentro (I) coincidono in un unico punto , detto centro del triangolo equilatero.

Passiamo alle caratteristiche del triangolo rettangolo

·      Poiché la somma degli angoli interni di un triangolo è 180° ed un angolo è retto, gli atri due angoli sono complementari, la loro somma è cioè 90°

·      Se un triangolo rettangolo ha un angolo acuto di 45° anche l’altro angolo acuto quindi sarà di 45°: il triangolo rettangolo sarà anche isoscele con i due cateti congruenti.

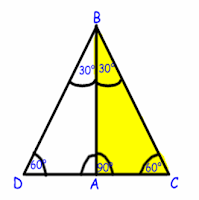
·      Se un triangolo rettangolo ha un angolo acuto di 30°, l’altro angolo acuto sarà di 60°: possiamo considerare questo triangolo come la metà di in triangolo equilatero che ha i lati della stessa lunghezza dell’ipotenusa. Nel triangolo equilatero l’altezza BA è anche mediana e bisettrice, quindi A è il punto medio di DC: ne deriva che il cateto AC opposto all’angolo di 30° è la metà dell’ipotenusa BC

Sappiamo che due triangoli sono congruenti se, sovrapponendoli, coincidono perfettamente. 

Esistono però dei criteri per riconoscere la congruenza tra triangoli senza la necessità di procedere a sovrapposizioni.

Il I criterio di congruenza dei triangoli afferma che due triangoli sono congruenti se hanno rispettivamente congruenti due lati e l’angolo tra essi compreso.

Il II criterio di congruenza dei triangoli afferma che due triangoli sono congruenti se hanno rispettivamente congruenti un lato ed i due angoli ad esso adiacenti.

Il III criterio di congruenza dei triangoli afferma che due triangoli sono congruenti se hanno rispettivamente congruenti i tre lati.

ESERCIZI

·    Completa le frasi relative alle caratteristiche del triangolo rettangolo

I due angoli acuti sono …………………………..

Se un angolo acuto è ampio 45°, l’altro angolo acuto misurerà …….. ° e quindi il triangolo è anche ………………………

Se un angolo acuto è ampio 30°, l’altro angolo acuto misurerà ………. ° ed il cateto opposto all’angolo di 30° ………………………………………………………………………………

·    Completa le frasi relative alle caratteristiche del triangolo isoscele

I lati obliqui sono …………………….

Gli angoli alla base sono …………………………..

L’altezza, l’asse, la mediana e la bisettrice relativi alla base …………………………………

…………………………………………………………………………………………………

Ortocentro, circocentro, baricentro ed incentro sono punti che si trovano ……………………

…………………………………………………………………………………………………

·    Completa le frasi relative alle caratteristiche del triangolo equilatero

I tre lati sono ………………………….

I tre angoli sono …………………………. e misurano ciascuno ……….. °

E’ un poligono regolare perché ……………………………………………………………

L’altezza, l’asse, la mediana e la bisettrice relativi ad un qualunque lato ……………………

…………………………………………………………………………………………………

Ortocentro, circocentro, baricentro ed incentro coincidono ………………………………, detto ………… del triangolo equilatero.

·    Considera le misure conosciute di questi due triangoli e spiega se sono congruenti ed in base a quale criterio:

triangolo ABC: AB = 8 cm – BC = 10 cm - angolo in B = 52°

triangolo FGH: FG = 8 cm – GH = 10 cm - angolo in G = 52°

·    Considera le misure conosciute di questi due triangoli rettangoli e spiega se sono congruenti ed in base a quale criterio:

triangolo ABC: cateto AB = 12 cm – cateto BC = 15 cm 

triangolo DEF: cateto DE = 12  cm – cateto EF = 15 cm 

·    Considera le misure conosciute di questi due triangoli e spiega se sono congruenti ed in base a quale criterio:

triangolo ABC: AB = 16 cm – BC = 21 cm - AC = 29 cm

triangolo CDE: CD = 16 cm – DE = 21 cm - CE = 29 cm

·    Di un triangolo ottusangolo ABC con BH altezza relativa al lato AC, conosciamo questi dati:

BC = 20 cm

AB = 6,2 cm

AH = HC – 15

P = 50,2 cm

b =  125 °

g = 10°

a)      Trova l’ampiezza dell’angolo a

b)      Trova l’ampiezza degli angoli interni del triangolo HBA e del triangolo BCH

c)      Che tipo di triangolo è HBA?

d)      Calcola il perimetro del triangolo HBA e del triangolo BCH