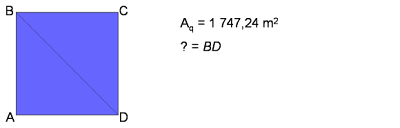Applicazioni del Teorema di Pitagora
Il teorema di Pitagora si applica solo ai triangoli rettangoli, ma la sua conoscenza può essere utile in tutti quei casi in cui in una figura piana è possibile ricavare un triangolo rettangolo.
Vediamo qualche esempio.
Triangolo equilatero
Tracciando l’altezza di un triangolo equilatero otteniamo due triangoli rettangoli. Consideriamone uno.
Abbiamo:
AB = ipotenusa (il lato del triangolo equilatero corrisponde all’ipotenusa)
BH = cateto (l’altezza del triangolo equilatero corrisponde ad un cateto)
AH = cateto (metà del lato del triangolo equilatero corrisponde all’altro cateto)
Proviamo a risolvere:
Un triangolo rettangolo ha il perimetro di 78 cm. Calcola la sua area.
(78 : 3) cm = 26 cm misura dei lati AB, BC, AC
(26 : 2) cm = 13 cm misura di AH
(26 x 22,51) : 2 cm2 = 292,63 cm2 area del triangolo ABC
Triangolo isoscele
Tracciando l’altezza di un triangolo isoscele otteniamo due triangoli rettangoli. Consideriamone uno.
Abbiamo:
AB = ipotenusa (il lato del triangolo isoscele corrisponde all’ipotenusa)
BH = cateto (l’altezza del triangolo isoscele corrisponde ad un cateto)
AH = cateto (metà della base del triangolo isoscele corrisponde all’altro cateto)
Proviamo a risolvere:
Un triangolo isoscele con l’area di 480 cm2, ha l’altezza lunga 30 cm. Calcola il perimetro del triangolo.
(480 x 2) : 30 cm = 32 cm misura della base AC
(32 : 2) cm = 16 cm misura di AH
(34 x 2) + 32 = 100 cm perimetro del triangolo ABC
Quadrato
Tracciando una diagonale del quadrato otteniamo due triangoli rettangoli isosceli , cioè con i cateti della stessa misura. Consideriamone uno.
Abbiamo:
BD = ipotenusa (la diagonale corrisponde all’ipotenusa)
AD = AB = cateti (i lati del quadrato corrispondono ai cateti)
Proviamo a risolvere:
Un quadrato ha la superficie che misura 1747,24 m2. Calcola la misura della diagonale.
Rettangolo
Tracciando una diagonale del rettangolo otteniamo due triangoli rettangoli. Consideriamone uno, il triangolo ABD.
Abbiamo:
AB = cateto (l’altezza del rettangolo corrisponde ad un cateto)
AD = cateto (la base del rettangolo corrisponde all’altro cateto)
BD = ipotenusa (la diagonale del rettangolo corrisponde all’ipotenusa)
Proviamo a risolvere:
Un rettangolo ha il perimetro di 252 cm e l’altezza è i 3/11 della base. Calcola l’area e la misura della diagonale.
(252 : 2) cm = 126 cm semiperimetro
3/11 + 11/11 = 14/11 = 126 cm
(126: 14) cm = 9 cm valore di 1/11
(9 x 3) cm = 27 cm misura dell’altezza AB
(9 x 11) cm = 99 cm misura della base AD
(99 x 27) cm2 = 2 673 cm2 area del rettangolo
Romboide
Tracciando le altezze del romboide otteniamo due triangoli rettangoli. Consideriamone uno, il triangolo ABH.
Abbiamo:
BH = cateto (l’altezza del romboide corrisponde ad un cateto)
AH = cateto
AB = ipotenusa (il lato obliquo del romboide corrisponde all’ipotenusa)
Proviamo a risolvere:
Un romboide con la base di 54 cm ha l’area di 1296 cm2. L’altezza divide la base in due parti una doppia dell’altra. Calcola il perimetro del romboide.
(1296 : 54) cm = 24 cm misura di BH
(54 : 3) cm = 18 cm misura di AH
(54 x 2) + (30 x 2) cm = 168 cm perimetro
Rombo
Tracciando le due diagonali del rombo otteniamo quattro triangoli rettangoli. Consideriamone uno, il triangolo ABE.
Abbiamo:
BE = cateto (metà della diagonale maggiore corrisponde ad un cateto)
AE = cateto (metà della diagonale minore corrisponde all’altro cateto)
AB = ipotenusa (il lato del rombo corrisponde all’ipotenusa)
Proviamo a risolvere:
In un rombo la somma della lunghezza delle due diagonali misura 392 cm, una diagonale è i ¾ dell’altra. Calcolare perimetro, area ed altezza del rombo.
¾ + 4/4 = 7/4 = 392 cm
(392 : 7) cm = 56 cm valore di ¼
(56 x 3) cm = 168 cm misura della diagonale minore AC
(56 x 4) cm = 224 cm misura della diagonale maggiore BD
(168 : 2) cm = 84 cm misura di AE
(224 : 2) cm = 112 cm misura di BE
(140 x 4) cm = 560 cm misura del perimetro
(224 x 168) : 2 cm2 = 18816 cm2 area del rombo
(18816 : 140) cm = 134,4 cm misura di CF, altezza del rombo
Trapezio rettangolo
Tracciando l’altezza di un trapezio rettangolo otteniamo un triangolo rettangolo. Consideriamo il triangolo rettangolo CHD.
Abbiamo:
CH = cateto (l’altezza del trapezio corrisponde ad un cateto)
HD = cateto (la differenza tra base maggiore e base minore corrisponde all’altro cateto)
CD = ipotenusa (il lato obliquo del trapezio corrisponde all’ipotenusa)
Proviamo a risolvere:
Di un trapezio rettangolo conosciamo la misura della base minore, 60 cm e la misura della diagonale minore, 68 cm . Sappiamo anche che il lato obliquo è i 2/3 della base minore. Calcoliamo il
perimetro di un rettangolo equivalente al trapezio e con la base di 64 cm.
(60 : 3) x 2 cm = 40 cm misura di CD
(60 + 24) cm = 84 cm misura di AD
(84 + 60) x 32 : 2 cm2 = 2304 cm2 misura dell’area del trapezio e del rettangolo
(2304 : 64) cm = 36 cm misura dell’altezza EF del rettangolo
(64 x 2) + (36 x 2) cm = 200 cm perimetro del rettangolo
Trapezio isoscele
Tracciando le altezze di un trapezio isoscele otteniamo due triangoli rettangoli. Consideriamone uno, il triangolo rettangolo ABH.
Abbiamo:
BH = cateto (l’altezza del trapezio corrisponde ad un cateto)
AH = cateto (la metà della differenza tra base maggiore e base minore corrisponde all’altro cateto)
AB = ipotenusa (il lato obliquo del trapezio corrisponde all’ipotenusa)
Proviamo a risolvere:
In un trapezio isoscele la base maggiore, l’altezza ed una diagonale misurano rispettivamente 280 cm, 150 cm e 250 cm. Calcola il perimetro e l’area del trapezio.
Consideriamo il triangolo rettangolo ACK.
Troviamo la lunghezza del segmento KD = AH
(280 – 200) cm = 80 cm misura di KD e AH
Troviamo la lunghezza della base minore
280 – (80 x 2) cm = 120 cm misura di BC
Ora possiamo trovare la misura del lato obliquo
Possiamo calcolare il perimetro
280 + 120 + (170 x 2) cm = 740 cm perimetro
Possiamo calcolare l’area
(280 + 120) x 150 : 2 = 30 000 cm2 area
ESERCIZI
· Il quadrilatero
ABCD è formato dal triangolo rettangolo ABD e dal triangolo isoscele BCD. Il cateto minore e l’ipotenusa del triangolo rettangolo misurano rispettivamente 15 cm e 25 cm, mentre il lato obliquo
del triangolo isoscele misura 12,5 cm. Calcola il perimetro e l’area del quadrilatero.
· Un quadrato con il
lato lungo 300 cm ed un triangolo isoscele formano un pentagono come vedi in figura. Se l’area del pentagono è 102 000 cm2, qual è il perimetro del pentagono?
· Un triangolo
rettangolo con i cateti lunghi 140 cm e 48 cm ha lo stesso perimetro di un rettangolo con la base di 56 cm. Calcola l’area e la diagonale del rettangolo (approssima ai decimi).
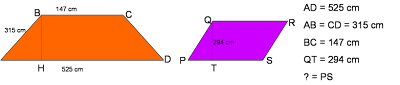
· Un trapezio
isoscele ha la base maggiore di 525 cm e la base minore di 147 cm, mentre il lato obliquo misura 315 cm. Calcola la base di un romboide equivalente al trapezio e con l’altezza di 294
cm.