Rapporti e proporzioni
Consideriamo questa situazione in cui ci vengono presentati due dati.
La popolazione della Campania è di 5 790 187 abitanti; la superficie della Campania è di 13 590 km2.
Possiamo mettere in relazione questi due dati, cioè rapportarli tra di loro per calcolare la densità di popolazione della Campania.
5 790 187 ab : 13 590 km2 = 426 abitanti per ogni km2
Vediamo che la ricerca del rapporto tra i due dati di partenza si è concretizzato in una divisione ed il quoziente tra i due dati è il loro rapporto numerico.
Possiamo dunque generalizzare affermando che il rapporto tra due numeri a e b è il quoziente di a : b.
Il rapporto tra due numeri, ad esempio 7 e 8 può essere indicato in modo diverso:
- con una divisione 7 : 8 (si legge “rapporto 7 a
8”)
- con una frazione 7/8 (si legge “rapporto sette
ottavi”)
- con un numero decimale 7 : 8 = 0,875 (si legge
“rapporto 0,875”)
I due numeri 7 e 8 si chiamano termini del rapporto: il primo termine prende il nome di antecedente, il secondo termine di conseguente.
Consideriamo ora questa situazione.
In una serie di tiri liberi a canestro Giorgio realizza 15 canestri in 20 tiri mentre Paolo realizza 12 canestri su 16 tiri.
Chi è stato il miglior tiratore? Non lasciamoci ingannare dal fatto che Giorgio ha fatto più canestri di Paolo, dobbiamo considerare per ogni giocatore il rapporto canestri fatti/tiri
effettuati.
Per Giorgio il rapporto è 15 : 20 = 0,75
Per Paolo il rapporto è 12 : 16 = 0,75
I due rapporti sono uguali, quindi i due giocatori hanno dimostrato uguale bravura.
Possiamo dunque scrivere così
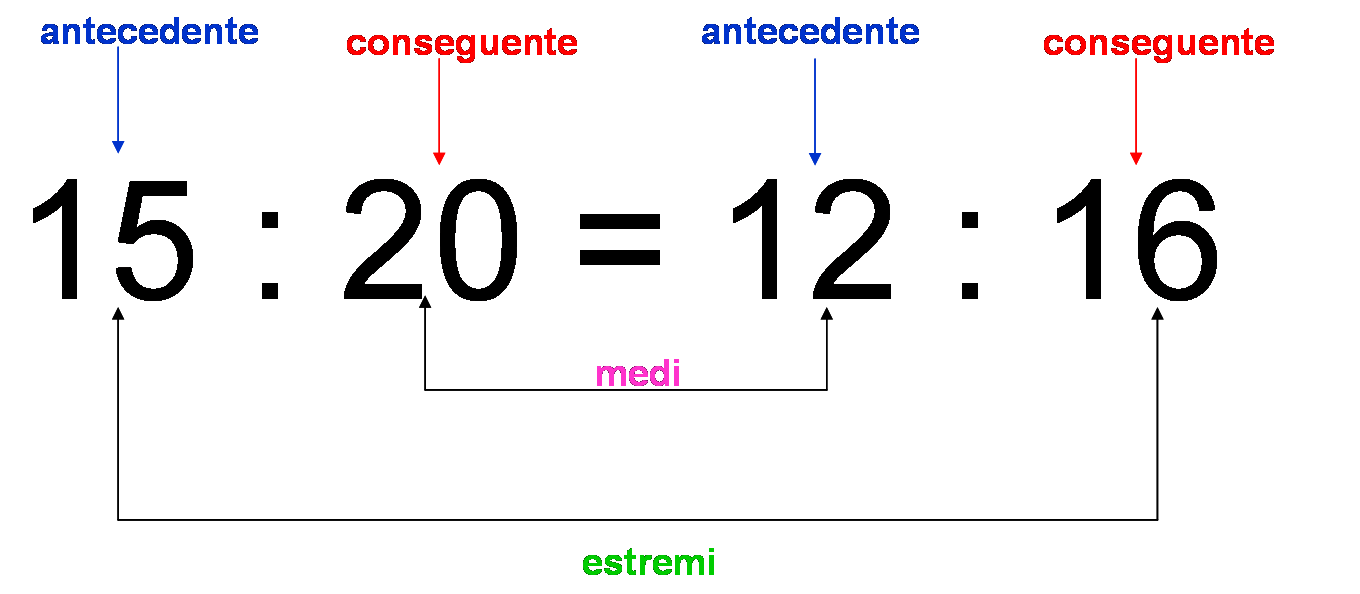
15 : 20 = 12 : 16
Abbiamo scritto un’uguaglianza fra due rapporti. Questa uguaglianza si chiama proporzione, che possiamo dunque definire come l’uguaglianza di due rapporti.
La proporzione sopra indicata si legge: 15 sta a 20 come 12 sta a 16.
Impariamo la nomenclatura corretta delle proporzioni:
- i quattro numeri sono
i termini della proporzione
- il 1° ed il 3° numero sono
gli antecedenti
- il 2° ed il 4° numero sono
i conseguenti
- il 1° ed il 4° numero sono
gli estremi
- il 2° ed il 3° numero sono
i medi
Tutte le proporzioni godono di alcune proprietà. Cominciamo ad esaminare la proprietà fondamentale.
La proprietà fondamentale delle proporzioni afferma che in ogni proporzione il prodotto dei medi è sempre uguale al prodotto degli estremi. Se la proporzione è a : b = x :
y avremo che a . y = b . x.
Nella proporzione 15 : 20 = 12 : 16 avremo che 15 . 16 = 20 . 12
Questa proprietà è utile per controllare se due rapporti possono formare una proporzione.
Esempio:
I rapporti 1,5 : 0,3 e 2,5 : 0,5 possono formare una proporzione?
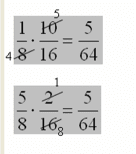
Moltiplichiamo gli estremi: 1,5 . 0,5 = 0,75
Moltiplichiamo i medi: 0,3 . 2,5 = 0,75
Sì, i due rapporti possono formare una proporzione.
Vediamo un altro esempio:
No, i due rapporti non formano una proporzione.
Passiamo ad esaminare un’altra proprietà, la cosiddetta proprietà dell’invertire.
La proprietà dell’invertire afferma che, in ogni proporzione, scambiando ogni antecedente con il proprio conseguente si ottiene ancora una proporzione.
Se la proporzione è a : b = c : d sarà una proporzione anche b : a = d : c.
Vediamo un esempio:
se è vero che 50 : 5 = 20 : 2 sarà anche vero che 5 : 50 = 2 : 20
Vediamo ora la proprietà del permutare.
La proprietà del permutare afferma che, in ogni proporzione, scambiando tra loro gli estremi o i medi o entrambi si ottengono altre proporzioni.
Se la proporzione è a : b = c : d saranno proporzioni anche
Un’altra proprietà delle proporzioni è la proprietà del comporre.
La proprietà del comporre afferma che, in ogni proporzione, la somma del 1° e 2° termine sta al 1° o al 2° termine come la somma del 3° e 4° termine sta al 3° o 4° termine.
Se è vera la proporzione a : b = c : d saranno proporzioni vere anche
(a + b) : a = (c + d) : c
(a + b) : b = (c + d) : d
Vediamo un esempio numerico. Se
Possiamo controllare con la proprietà fondamentale che ciò che abbiamo ottenuto è veramente una proporzione.
Applichiamo la proprietà del comporre nel secondo modo.
Vediamo infine la proprietà dello scomporre.
La proprietà dello scomporre afferma che, in ogni proporzione che abbia gli antecedenti maggiori dei rispettivi conseguenti, la differenza tra il 1° e 2° termine sta al 1° o al 2°
termine come la differenza tra il 3° e 4° termine sta al 3° o 4° termine.
Se è vera la proporzione a : b = c : d saranno proporzioni vere anche
(a - b) : a = (c - d) : c
(a - b) : b = (c - d) : d
Vediamo un esempio numerico. Se
Possiamo controllare con la proprietà fondamentale che ciò che abbiamo ottenuto è veramente una proporzione.
Applichiamo la proprietà dello scomporre nel secondo modo.
ESERCIZI
· Quali, tra
questi rapporti, possono costituire una proporzione?
12 : 3 e 14 : 2
36 : 6 e 30 : 5
200 : 20 e 30 : 3
100 : 2 e 200 : 20
· Data la
proporzione 25 : 20 = 30 : 24 rispondi alle domande:
- Quali sono gli antecedenti?
- Quali sono i conseguenti?
- Quali sono gli estremi?
- Quali sono i medi?
- Qual è il valore del rapporto?
· Ad ogni
proporzione applica le proprietà dell’invertire, del permutare, del comporre e dello scomporre (quando possibile)
|
|
Proprietà dell’invertire
|
Proprietà del permutare
|
Proprietà del comporre
|
Proprietà dello scomporre
|
|
5 : 7 = 15 : 21
|
|
|
|
|
|
54 : 6 = 18 : 2
|
|
|
|
|
|
72 : 12 = 36 : 6
|
|
|
|
|
|
3 : 4 = 9 : 12
|
|
|
|
|