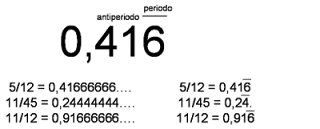Vediamo quali sono le situazioni che possiamo incontrare calcolando il valore di una frazione, cioè il quoziente tra il numeratore ed il denominatore.

Vediamo il caso in cui la frazione è apparente.

14/7 = 2                      40/5 = 8

Se la frazione è apparente si trasformerà in un numero intero.

Consideriamo ora le frazioni decimali.

32/100 = 0,32             53/10 = 5,3                 165/1000 = 0,165

Se la frazione è decimale si trasforma in un numero decimalelimitato, perché ha un numero di cifre decimali limitato.

  

Consideriamo ora frazioni non decimali, cioè frazioni ordinarie con denominatore diverso da 10 o da una potenza di 10

3/8 = 0,375                                         7/20 = 0,35                             135/50 = 2,7

4/11 = 0,36363636…….                    8/15 = 0,533333333…..         6/13 = 0,461538461538…….

Possiamo osservare come il primo gruppo di frazioni ordinarie si trasformi in numeri decimali limitati mentre il secondo gruppo dà origine a numeri decimali illimitati perché la divisione tra numeratore e denominatore, anche se proseguita, non avrà mai resto zero, quindi il numero delle cifre decimali del quoziente è illimitato.

Come possiamo sapere se una frazione ordinaria darà origine ad un numero decimale limitato o illimitato? E’ semplice, basta scomporre in numeri primi il suo denominatore.

Facciamolo per il primo gruppo di frazioni:

8 =  2³                 20 = 2² x 5                  50 = 2 x 5²

Scomponiamo ora il denominatore del secondo gruppo di frazioni:

11 = 11           15 = 3 x 5                   13 = 13

Una frazione ordinaria irriducibile si trasforma in un numero decimale limitato solo nei casi in cui la scomposizione in fattori primi del denominatore contenga esclusivamente il fattore 2, il fattore 5 o entrambi i fattori.

Bene, centriamo ora la nostra attenzione sui numeri decimali illimitati.

Consideriamo queste frazioni e calcoliamone il valore: 5/9, 10/3, 3/11, 2/27, 5/12, 11/45, 11/12

5/9 = 0,55555……

10/3 = 3,333333…..

3/11 = 0,27272727……

2/27 = 0,074074074……

5/12 = 0,41666666….

11/45 = 0,24444444….

11/12 = 0,91666666….

Vediamo che tutte queste frazioni si trasformano in numeri decimali illimitati. Consideriamo le prime quattro frazioni.

5/9 = 0,55555……

10/3 = 3,333333…..

3/11 = 0,27272727……

2/27 = 0,074074074……

Possiamo vedere come, subito dopo la virgola, una cifra o un gruppo di cifre si ripete all’infinito: la cifra o il gruppo di cifre che si ripete si chiama periodo ed i numeri sono detti numeri decimali illimitati periodici semplici. Per indicare il periodo si mette una lineetta sopra la cifra o il gruppo di cifre che si ripete.

Una frazione irriducibile si trasforma in un numero decimale illimitato periodico semplice se nella scomposizione in fattori primi del denominatore non è presente né il fattore 2 né il fattore 5.

Consideriamo ora le altre tre frazioni.

5/12 = 0,41666666….

11/45 = 0,24444444….

11/12 = 0,91666666….

Vediamo come, in questi casi, il periodo non inizi subito dopo la virgola in quanto tra la virgola ed il periodo è presente una cifra o un gruppo di cifre. Questi numeri sono detti numeri decimali illimitati periodici misti.

La cifra o il gruppo di cifre tra la virgola ed il periodo si chiama antiperiodo e si scrive in questo modo

Una frazione irriducibile si trasforma in un numero decimale illimitato periodico misto se nella scomposizione in fattori primi del denominatore è presente il fattore 2 o  il fattore 5 o entrambi oltre ad altri fattori primi.

Possiamo quindi rappresentare così l’insieme Q⁺

Possiamo sintetizzare così ciò che si ottiene nelle varie possibilità di trasformazione di una frazione in numero:

ESERCIZI

·        Quando un numero decimale si può definire limitato?

·        Quando una frazione ordinaria irriducibile può essere trasformata in un numero decimale limitato?

·        Quando un numero si dice decimale illimitato periodico semplice?

·        Quando un numero si dice decimale illimitato periodico misto?

·        Per ogni numero indica se è un numero decimale limitato, illimitato periodico semplice o illimitato periodico misto. 

·        Individua, tra le seguenti frazioni, quali possono essere trasformate in numeri decimali limitati ed esegui la trasformazione

4/21, 11/25, 51/50, 13/20, 18/100, 27/70, 19/30, 2/5

·        Individua, tra le seguenti frazioni, quali possono essere trasformate in numeri decimali illimitati periodici semplici ed esegui la trasformazione

22/15; 5/9; 6/11; 11/18; 32/3; 25/12; 25/9; 7/100

·        Individua, tra le seguenti frazioni, quali possono essere trasformate in numeri decimali illimitati periodici misti ed esegui la trasformazione

5/8; 5/12; 13/45; 6/5; 13/6; 7/3; 5/18; 11/12