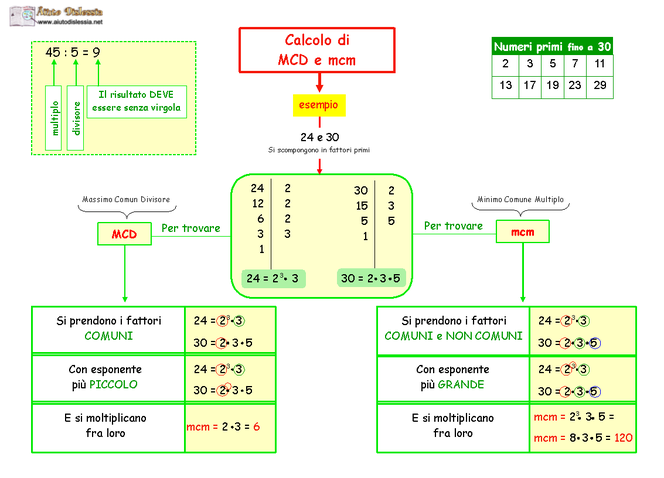
IL M.C.D.

Che cos’è il Massimo Comune Divisore?
Il Massimo Comune Divisore fra due o più numeri è il maggiore tra i divisori comuni ai numeri dati. Il Massimo Comune Divisore si abbrevia
con M.C.D.
Es: qual è il M.C.D. tra 24 e 16?
Cerchiamo tutti i divisori di 24
D (24) = {1, 2, 3, 4, 6, 8, 12, 24}
Cerchiamo tutti i divisori di 16
D (16) = {1, 2, 4, 8, 16}
I due numeri 24 e 16 hanno dei divisori comuni: 1, 2, 4, 8. Il maggiore di questi divisori è 8, quindi il M.C.D. (24, 16) = 8
Esistono sistemi diversi per calcolare il M.C.D. fra due o più numeri. Noi qui ne presentiamo due.
· Cominciamo ad
esaminare il cosiddetto metodo insiemistico.
Vogliamo trovare il M.C.D. fra 65, 140 e 90.
Elenchiamo tutti i divisori di 65.
D (65) = {1, 5, 13, 65}
Elenchiamo tutti i divisori di 140.
D (140) = {1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}
Elenchiamo tutti i divisori di 90.
D (90) = {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90}
Calcoliamo l’insieme dei divisori comuni, cioè l’intersezione tra gli elementi dei tre insiemi precedenti.
D (65) ÇD (140) ÇD (90) = {1,
5,}
M.C.D. (65, 140, 90) = 5
Vediamo un altro esempio
Vogliamo trovare il M.C.D. fra 140, 105 e 35.
Elenchiamo tutti i divisori di 140.
D (140) = {1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}
Elenchiamo tutti i divisori di 105.
D (105) = {1, 3, 5, 7, 15, 21, 35, 105}
Elenchiamo tutti i divisori di 35.
D (35) = {1, 5, 7, 35}
Calcoliamo l’insieme dei divisori comuni, cioè l’intersezione tra gli elementi dei tre insiemi precedenti.
D (140) ÇD (105) ÇD (35) = {1,
5, 7, 35}
M.C.D. (140, 105, 35) = 35
Possiamo quindi dire che con il metodo insiemistico, per calcolare il M.C.D. tra due o più numeri, si elencano gli insiemi dei divisori dei numeri dati, si calcola l’insieme intersezione e il
M.C.D. sarà l’elemento maggiore dell’insieme intersezione.
· Esaminiamo ora il
cosiddetto metodo della scomposizione in fattori primi, raccomandabile soprattutto se i numeri sono grandi.
Vogliamo trovare il M.C.D. fra 288, 360 e 186.
Scomponiamo in fattori primi i tre numeri
|
288
|
2
|
|
144
|
2
|
|
72
|
2
|
|
36
|
2
|
|
18
|
2
|
|
9
|
3
|
|
3
|
3
|
|
1
|
|
288 = 25 x 32
|
360
|
2
|
|
180
|
2
|
|
90
|
2
|
|
45
|
3
|
|
15
|
3
|
|
5
|
5
|
|
|
|
360 = 23 x 32 x 5
|
186
|
2
|
|
93
|
3
|
|
31
|
31
|
|
1
|
|
186 = 2 x 3 x 31
Vediamo ora se ci sono fattori primi comuni ai tre numeri e consideriamoli col minore esponente.
288 = 25 x 32
360 = 23 x 32 x 5
186 = 2 x 3 x 31
I fattori comuni, presi con il minore esponente, sono 2 e 3, quindi
M.C.D. (288, 360, 186) = 2 x 3 = 6
Vediamo un altro esempio
Vogliamo trovare il M.C.D. fra 528, 624, 768.
Scomponiamo in fattori primi i tre numeri
|
528
|
2
|
|
264
|
2
|
|
132
|
2
|
|
66
|
2
|
|
33
|
3
|
|
11
|
11
|
|
1
|
|
528 = 24 x 3 x 11
|
624
|
2
|
|
312
|
2
|
|
156
|
2
|
|
78
|
2
|
|
39
|
3
|
|
13
|
13
|
|
1
|
|
624 = 24 x 3 x 13
|
768
|
2
|
|
384
|
2
|
|
192
|
2
|
|
96
|
2
|
|
48
|
2
|
|
24
|
2
|
|
12
|
2
|
|
6
|
2
|
|
3
|
3
|
|
1
|
|
768 = 28 x 3
Vediamo ora se ci sono fattori primi comuni ai tre numeri e consideriamoli col minore esponente.
528 = 24 x 3 x 11
624 = 24 x 3 x 13
768 = 28 x 3
I fattori comuni, presi con il minore esponente, sono 24 e 3, quindi
M.C.D. (288, 360, 186) = 24 x 3 = 16 x 3 = 48
Possiamo quindi dire che con il metodo della scomposizione in fattori primi, per calcolare il M.C.D. tra due o più numeri, si scompongono i numeri dati in fattori
primi e il M.C.D. sarà il prodotto dei fattori comuni considerati con il minore esponente.
Vediamo un altro esempio
Vogliamo trovare il M.C.D. fra 9, 12, 14.
Scomponiamo in fattori primi i tre numeri
|
9
|
3
|
|
3
|
3
|
|
1
|
|
9 = 32
|
12
|
2
|
|
6
|
2
|
|
3
|
3
|
|
1
|
|
12 = 22 x 3
|
14
|
2
|
|
7
|
7
|
|
1
|
|
14 = 2 x 7
Vediamo ora se ci sono fattori primi comuni ai tre numeri e consideriamoli col minore esponente.
9 = 32
12 = 22 x 3
14 = 2 x 7
I tre numeri non hanno altri divisori comuni, oltre ad 1, quindi il M.C.D. è 1 e questi numeri si dicono primi tra loro.
ESERCIZI
· Che cos’è il
M.C.D. fra due o più numeri?
· Quando due o
più numeri si dicono primi tra loro?
· Calcola il
M.C.D. dei seguenti gruppi di numeri, usando il metodo insiemistico:
a) 70, 42,
98; b) 56,
42, 24;
c) 32,
30; d) 18,
20, 30
· Calcola il
M.C.D. dei seguenti gruppi di numeri usando il metodo della scomposizione in fattori primi:
a) 60,
75; b) 252,
270;
c) 3 150, 3 675; d) 72, 128, 216;
e) 324, 729, 486; f) 190, 380, 684;
g) 180, 300, 528, 672; h) 128, 220, 286,
308;
