LE FRAZIONI

Il contenuto YouTube non può essere visualizzato a causa delle impostazioni dei cookie. Per acconsentire al caricamento e alla visualizzazione del contenuto YouTube devi accettare i cookie funzionali di YouTube dal relativo banner.


Sappiamo già che frazionare significa suddividere in parti uguali un intero che può essere costituito da una quantità continua o discontinua.
Consideriamo un rettangolo intero e dividiamolo in 6 parti uguali.
Ognuna delle parti costituisce “un sesto” del rettangolo che indichiamo1/6
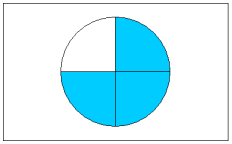
Vediamo ora un cerchio intero suddiviso in 4 parti uguali.
Ogni parte rappresenta “un quarto” e si indica 1/4
Poiché queste frazioni rappresentano una ed una sola delle parti in cui abbiamo diviso la grandezza intera, diremo che 1/6 e 1/4 sono unità frazionarie.
Le unità frazionarie indicano quindi una sola delle parti in cui è diviso un intero.
Guardiamo ora questa figura
Vediamo che abbiamo considerato 4 volte l’unità frazionaria 1/6
1/6 + 1/6 + 1/6 + 1/6 = 4/6
Se invece osserviamo quest’altra figura
vediamo che abbiamo considerato 3 volte l’unità frazionaria ¼
¼ + ¼ + ¼ = ¾
4/6, ¾ sono frazioni
La frazione è quindi un operatore che divide un intero in parti uguali e ne considera alcune di esse.
Possiamo classificare le frazioni in: proprie, improprie, apparenti.
Guardiamo questo esempio
La frazione 3/5 rappresenta la parte colorata del rettangolo. Si tratta di una parte minore dell’intero.
La frazione 5/8 rappresenta la parte colorata dell’intero. Si tratta di una parte minore dell’intero.
3/5 e 5/8 sono frazioni proprie.
Una frazione è propria quando, operando con essa su una grandezza, otteniamo una grandezza minore di quella di partenza. Riconosciamo le frazioni proprie perché il numeratore è minore del
denominatore.
Osserviamo ora questi esempi
La frazione 7/5 rappresenta la parte colorata. Si tratta di una parte maggiore del rettangolo intero.
La frazione 5/4 rappresenta la parte colorata. Si tratta di una parte maggiore del cerchio intero.
7/5 e 5/4 sono frazioni improprie.
Una frazione è impropria quando, operando con essa su una grandezza, otteniamo una grandezza maggiore di quella di partenza. Riconosciamo le frazioni improprie perché il numeratore è maggiore
(ma non multiplo) del denominatore.
Consideriamo ora quest’altro esempio
La frazione 5/5 rappresenta la parte colorata e corrisponde all’intero.
La frazione 12/4 rappresenta la parte colorata e corrisponde a 3 interi.
5/5 e 12/4 sono frazioni apparenti.
Una frazione è apparente quando, operando con essa su una grandezza, otteniamo una grandezza congruente o multipla di quella di partenza. Riconosciamo le frazioni apparenti perché il
numeratore è uguale o multiplo del denominatore.
Abbiamo operato su una grandezza intera ed abbiamo ottenuto la frazione che rappresenta la parte colorata: 4/9
Abbiamo operato sulla stessa grandezza ed abbiamo ottenuto un’altra frazione che rappresenta la parte colorata: 5/9
Se consideriamo la somma delle due grandezze ottenute otteniamo una grandezza che è congruente alla grandezza di partenza. Infatti: 4/9 + 5/9 = 9/9
4/9 e 5/9 sono frazioni complementari.
Due frazioni sono complementari quando, operando con esse su una grandezza, otteniamo due grandezze la cui somma è congruente alla grandezza di partenza.
ESERCIZI
· Completa la
seguente tabella
|
Frazioni
|
Numeratore
|
Denominatore
|
Unità frazionaria
|
N° delle unità frazionarie considerate
|
|
4/5
|
|
|
|
|
|
|
5
|
7
|
|
|
|
6/13
|
|
|
|
|
|
3/7
|
|
|
|
|
|
|
4
|
9
|
|
|
· Quale unità
frazionaria rappresenta la parte colorata di ogni figura?
· Quale frazione
rappresenta la parte colorata di ogni figura?
· Quando possiamo
dire che due frazioni sono complementari?
· Fra le seguenti
coppie di frazioni cerchia quelle complementari
3/8 e 5/8; 5/10 e 4/10; 3/11 e 8/11; 2/9 e 5/9; 8/10 e 6/10; 3/7 e 4/7; 1/10 e 9/10; 13/20 e 7 /20
· Quando possiamo
dire che una frazione è propria?
· Quando possiamo
dire che una frazione è impropria?
· Quando possiamo
dire che una frazione è apparente?
· Considera
l’insieme:
e scrivi per elencazione i seguenti sottoinsiemi:
B = {x/x Î A ed è frazione propria}
C = {x/x Î A ed è frazione impropria}
D = {x/x Î A ed è frazione apparente}