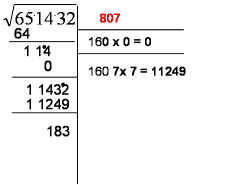La radice quadrata

L’estrazione di radice è il procedimento che ci permette di trovare la base, conoscendo l’esponente ed il valore di una potenza. Si tratta quindi dell’operazione inversa rispetto all'elevamento a potenza.
Come l’elevamento a potenza può essere alla seconda, alla terza, alla quarta ……, così l’estrazione di radice può essere quadrata, cubica, ecc.
Per ora consideriamo l’estrazione di radice quadrata (per convenzione si omette l’indice 2 sopra il segno di radice)
Dovrebbe essere evidente che 
Vediamo il nome dei termini di questa operazione

Possiamo dunque dire che l’estrazione della radice quadrata di un numero (radicando) consiste in un’operazione che permette di individuare un altro numero che, elevato al quadrato, dà come risultato il radicando.
I quadrati perfetti
Osserviamo alcuni casi:


I numeri per cui esiste la radice quadrata perfetta si dicono quadrati perfetti e la loro radice quadrata è esatta.
Come possiamo fare per riconoscere se un numero è un quadrato perfetto? Scomponiamo in fattori primi alcuni dei numeri che abbiamo visto o che sappiamo essere quadrati perfetti.
49
7
7
7
1
81
3
27
3
9
3
3
3
1
64
2
32
2
16
2
8
2
4
2
2
2
1
100
2
50
2
25
5
5
5
1
49 = 72
81 = 34
64 = 26
100 = 22 x 52
Ci accorgiamo che tutti questi numeri sono uguali al prodotto di tutti fattori con esponenti pari. Possiamo dunque affermare che un numero è un quadrato perfetto quando è uguale al prodotto di fattori primi tutti con esponenti pari.
I numeri non quadrati perfetti
E i numeri che non sono quadrati perfetti? Di essi non possiamo trovare la radice quadrata esatta, ma possiamo calcolare la radice quadrata approssimata per difetto o per eccesso.

Consideriamo, ad esempio,  

Qual è il numero più grande che, elevato al quadrato, ci dà un numero inferiore a 55? E’ 7 perché 72 = 49 < 55
Qual è il numero più piccolo che, elevato al quadrato, ci dà un numero superiore a 55? E’ 8 perché 82 = 64 > 55
Quindi 7 è la radice quadrata di 55 approssimata per difetto a meno di una unità, invece 8 è la radice quadrata di 55 approssimata per eccesso a meno di una unità.
Estrazione di una radice quadrata
Passiamo ora ad illustrare il procedimento per l’estrazione di una radice quadrata.
Estraiamo la radice quadrata di 33 856.

Estraiamo ora la radice quadrata di 651 432

 

In questo caso, poiché l’ultimo resto è diverso da zero, non abbiamo una radice quadrata esatta, bensì una radice quadrata approssimata per difetto a meno di una unità.
ESERCIZI
·      Verifica, con la scomposizione in fattori primi, se i seguenti numeri sono quadrati perfetti.
1 440 – 1 444 - 3 240 –  5 184 - 12 348 – 14 400
·      Calcola la radice quadrata esatta dei seguenti numeri:
2 601 – 11 025 – 158 404 
·      Calcola la radice quadrata approssimata per difetto a meno di una unità dei seguenti numeri:
1029 – 11 235 – 516 986