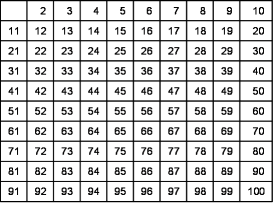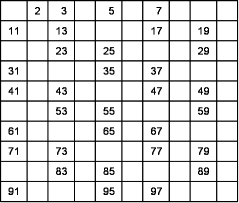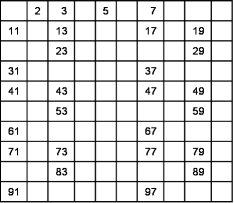LA DIVISIBILITA'
24 : 4 = 6 resto 0
25 : 3 = 8 resto 1
25 non è divisibile per 3
24 è divisibile per 4 e quindi 4 è un divisore di 24.
Generalizzando, possiamo dire che un numero x è divisibile per un numero y se x : y dà un numero esatto senza resto. Se così è possiamo anche
dire che:
x è divisibile per y, quindi x è un multiplo di y
y è un divisore di x, quindi y è un sottomultiplo di x.
I multipli di un numero sono infiniti, mentre i sottomultipli sono in numero finito.
Esistono dei criteri per stabilire in alcuni casi se un numero è divisibile per un altro.
Un numero è divisibile per 2 se termina con una cifra pari: 0, 2, 4, 6, 8
3 268 è divisibile per 2, 5 471 non è divisibile per 2.
Un numero è divisile per 3 se sommando tutte le sue cifre otteniamo un multiplo di 3
7 218 è divisibile per 3 perché 7 + 2 + 1 + 8 = 18 e 18 è un multiplo di 3
8 725 non è divisibile per 3 perché 8 + 7 + 2 + 5 = 22 e 22 non è un multiplo di 3
93 è divisibile per 3 perché 9 + 3 = 12 e 12 è un multiplo di 3.
Un numero è divisile per 4 se le ultime due cifre sono due “zeri” o sono multipli di 4
600 è divisibile per 4
4 328 è divisibile per 4
21 708 è divisibile per 4
32 861 non è divisibile per 4
Un numero è divisile per 5 se l’ultima cifra è 0 o 5
565 è divisibile per 5
3 450 è divisibile per 5
6 587 non è divisibile per 5
Per stabilire se un numero è divisibile per 11 dobbiamo sommare le cifre di posto dispari e quelle di posto pari: la differenza tra la somma delle cifre di posto dispari
e quella delle cifre di posto pari deve essere 0, 11 o un multiplo di 11
12 455 non è divisibile per 11 perché
1 + 4 + 5 = 10 2 + 5 = 7 10 – 7 = 3
638 è divisibile per 11 perché
6 + 8 = 14 14 – 3 = 11
46 695 è divisibile per 11 perché
4 + 6 + 5 = 15 6 + 9 = 15 15 – 15 = 0
359 294 804 è divisibile per 11 perché
3 + 9 + 9 + 8 + 4 = 33 5 + 2 + 4 + 0 =
11 33 – 11 = 22
Un numero naturale si dice primo se è divisibile solo per 1 e per se stesso. Un numero primo ha quindi solo 2 divisori: 1 e se stesso.
Il numero 1 non è considerato numero primo.
Entro il 10 i numeri primi sono 2, 3, 5, 7.
Il matematico e geografo Eratostene ideò quello che ancora oggi è forse il metodo più efficace per estrarre liste di numeri primi tra due numeri dati: il famoso crivello di
Eratostene. Se, ad esempio, vogliamo trovare i numeri compresi tra 1 e 100, scriviamo tutti i numeri dal 2 al 100.
Eliminiamo tutti i numeri multipli di 2 che non possono essere primi (lasciamo però il 2)
Eliminiamo tutti i multipli di 3 (lasciamo però il 3)
Eliminiamo tutti i multipli di 5 (lasciamo però il 5)
Eliminiamo tutti i multipli di 7 (lasciamo però il 7)
Eliminiamo tutti i multipli di 11 (lasciamo però l’11): ci accorgiamo che non ci sono multipli di 11. I numeri rimasti nella tabella sono i numeri primi compresi tra 1 e 100.
Esistono comunque liste già preparate di numeri primi (ricorda che anche i numeri primi sono infiniti): ecco un link per consultare una tabella dei numeri primi fino a 10 000
ESERCIZI
· Quando
possiamo dire che un numero a è divisibile per un numero b?
· Quando
possiamo dire che un numero a è sottomultiplo del numero b?
· Quando un
numero si dice primo?
· Al posto dei
puntini inserisci “è divisibile per” oppure “è divisore di”
54 ……………………………………………. 9
4 ……………………………………………. 32
13 ……………………………………………. 26
3 ……………………………………………. 18
6 ……………………………………………. 24
8 ……………………………………………. 4
· Quali tra
questi numeri sono divisibili per 2?
8178 7393 6954 1778 7417 3130 9909 5976 7718 5045
· Quali tra
questi numeri sono divisibili per 3? E quali sono divisibili contemporaneamente per 2 e per 3?
7431 818 2586 9021 8208 4171 8501 8515 3838 9113
· Quali tra
questi numeri sono divisibili per 4?
3636 7072 533 8009 718 6630 6738 6008 1100 4612
· Quali tra
questi numeri sono divisibili per 5? E quali sono divisibili contemporaneamente per 4 e per 5?
8500 2728 1935 1640 6382 6576 9815 6335 8803 9445
· Quali tra
questi numeri sono divisibili per 11?
5577 4577 5500 3550 444 9119
· In questa
serie di numeri quali sono i numeri primi?
21 76 3 57 65 92 100 7 89 13