Consideriamo gli insiemi numerici che conosciamo finora.

Abbiamo esaminato l’insieme N o insieme dei numeri naturali

{0, 1, 2, 3, 4,......}

 Abbiamo visto come l’addizione e la moltiplicazione siano operazioni interne all’insieme N mentre la sottrazione non è un’operazione interna all’insieme dei numeri naturali perché non è sempre possibile restando nell’ambito dei numeri naturali.

Per dare una risposta a qualsiasi sottrazione, i matematici hanno inventato i numeri relativi (con il segno), e cioè l’insieme Z.

{...,-4, -3, -2, -1, 0, 1, 2, 3, 4,......}

L’addizione, la sottrazione e la moltiplicazione sono operazioni interne all’insieme Z perché il risultato è sempre un numero intero relativo. La divisione, invece, non è un’operazione interna all’insieme Z perché in alcuni casi non è possibile: ad esempio (+3) : (+5) = ?

Per poter eseguire qualsiasi divisione, i matematici hanno inventato le frazioni: l’insieme Q⁺ o insieme dei numeri razionali.

-3/4                  +6/5              +5/2

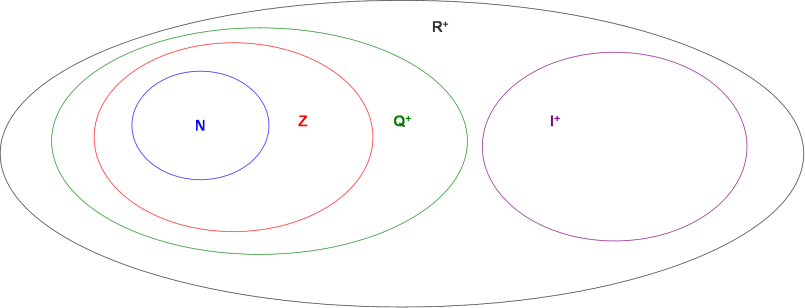
L’insieme Q⁺ include sia l’insieme N che l’insieme Z.

L’addizione, la sottrazione, la moltiplicazione e la divisione sono operazioni interne all’insieme Q⁺ perché il risultato è sempre un numero razionale relativo.

L’estrazione di radice non è sempre un’operazione interna all’insieme Q⁺: se il numero di cui dobbiamo estrarre la radice quadrato è un quadrato perfetto allora l’estrazione di radice è interna a Q⁺. 

Se invece il numero di cui vogliamo estrarre la radice quadrata non è un quadrato perfetto, sappiamo che otterremo una radice quadrata approssimata per difetto a meno di 0,1 – 0,01 – 0,001, ecc. Ad esempio la radice quadrata di 10 approssimata per difetto a meno di 0,00001 è 3,16227….. ma potremmo proseguire all’infinito ottenendo un numero decimale illimitato con cifre decimali che non si ripeteranno mai: si tratta quindi di un numero decimale illimitato non periodico. I numeri di questo tipo sono chiamati numeri irrazionali.

Per dare quindi una risposta a qualsiasi radice con radicando positivo, i matematici hanno inventato i numeri irrazionali: l’insieme I⁺ o insieme dei numeri irrazionali.

L’unione dell’insieme Q⁺ dei numeri razionali e dell’insieme I⁺ dei numeri irrazionali forma l’insieme R⁺ o insieme dei numeri reali assoluti.

L’estrazione di radice quadrata è un’operazione interna all’insieme R⁺.

Possiamo rappresentare graficamente in questo modo

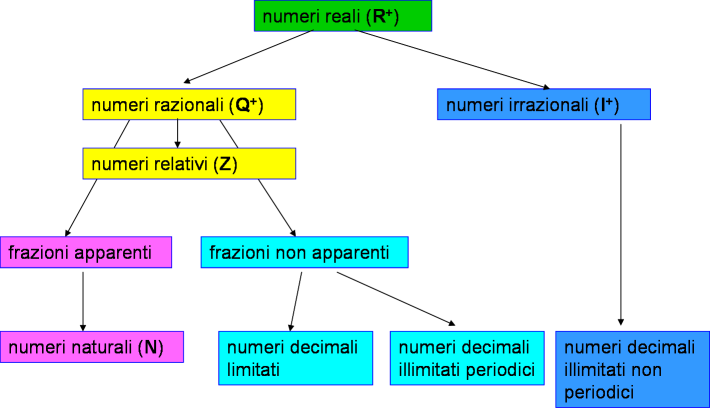
oppure anche così

ESERCIZI

·      La sottrazione è un’operazione interna all’insieme N?

·      La sottrazione è un’operazione interna all’insieme Z?

·      Quali sono le operazioni interne all’insieme Z?

·      L’estrazione di radice quadrata è un’operazione interna all’insieme Q⁺?

·      In quale insieme l’estrazione di radice quadrata è un’operazione interna?

·      Qual è l’insieme formato dall’unione dei numeri razionali e dall’insieme dei numeri irrazionali?

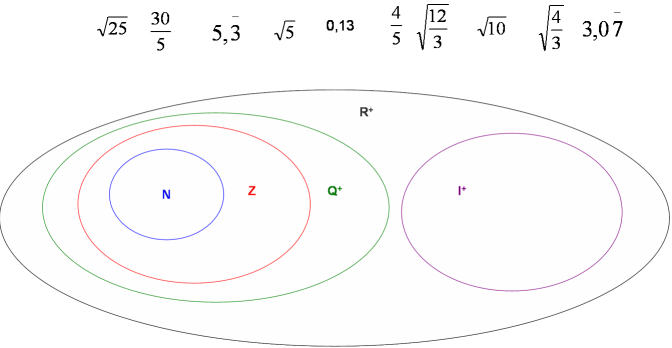
·      Inserisci i seguenti numeri al posto corretto nel diagramma di Eulero-Venn

·      Quali tra i seguenti numeri reali assoluti sono razionali e quali irrazionali? Cerchia di blu i razionali e di rosso gli irrazionali.