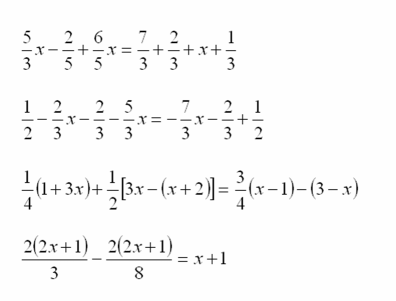Risoluzione di equazioni di I° grado
Sappiamo che la soluzione di un’equazione è data dal calcolo dei valori delle incognite che rendono vera l’equazione. Se consideriamo l’equazione 3x = 21 notiamo che il primo membro dell’equazione è formato da un unico termine, detto coefficiente della x, mentre il secondo membro è formato da un unico termine noto. Un’equazione di questo tipo si dice ridotta in forma normale.
Come possiamo risolvere un’equazione ridotta in forma normale? E’ sufficiente dividere il termine noto dell’equazione per il coefficiente dell’incognita.
3x = 21 x = 21/3 = 7
Vediamo alcuni altri esempi
E se l’equazione non è ridotta a forma normale? Occorre ridurla a forma normale seguendo alcune regole.
1) Occorre innanzitutto eliminare le parentesi eseguendo le operazioni indicate secondo le regole già note.
2) Se, come in questo caso, l’equazione è con termini frazionari, occorre ridurla a forma intera. A tal fine bisogna calcolare il m.c.m. dei denominatori; m.c.m. (3; 2) =
6 e successivamente moltiplicare ciascun membro dell’equazione per l’m.c.m.
3) Una volta ridotta l’equazione a forma intera, in virtù del 1° principio di equivalenza che ci consente di spostare qualsiasi termine da un membro all’altro cambiandolo di
segno, trasportiamo tutti i termini in x al 1° membro e tutti i termini noti al 2° membro.
4 + 3x + 18x – 18x + 12x = - 4 – 12 - 4
4) Ora eseguiamo l’addizione algebrica dei termini del 1° e del 2° membro, riducendo così l’equazione a forma normale.
3x + 18x – 18x + 12x = - 4 – 12 - 4
15x = -20
5) Risolviamo ora l’equazione dividendo il termine noto dell’equazione per il coefficiente dell’incognita.
Quando siamo nella fase 5 e quindi abbiamo l’equazione ridotta in forma normale
da risolvere, possono presentarsi questi casi, di cui ora proporremo un’esemplificazione:
a) Nell’equazione risolta sopra abbiamo
avuto al termine
La soluzione esiste ed è unica: l’equazione è determinata.
b) Immaginiamo di avere questa equazione ridotta a forma normale
Anche in questo caso a soluzione esiste ed è unica: l’equazione è determinata.
c) Immaginiamo di avere questa equazione ridotta a forma normale
0x = 15
x non può avere nessun valore perché non esiste un numero che moltiplicato per zero dia 15 o qualunque altro numero diverso da zero: l’equazione è impossibile.
d) Immaginiamo di avere questa equazione ridotta a forma normale
0x = 0
x può assumere il valore di qualsiasi numero perché qualsiasi numero moltiplicato per zero dà come risultato zero: l’equazione è indeterminataperché ha infinite soluzioni.
ESERCIZI
· Risolvi le seguenti equazioni
11x + 3 – 4 = 12x + 6 – 2x
4(x + 2) – 2x = 2(x + 6)
5x + 6(3x – 1) = 7x + 4(x – 2) + 1
3(6x – 4) + 12x = 5(4x + 1) + 10x – 17