Ricordiamo che, date due variabili x (variabile indipendente) ed y (variabile dipendente), possiamo dire che y è in funzione di x 

y = f(x)

se esiste una relazione per cui ad ogni valore della x corrisponde uno ed un solo valore della y.

Se questa relazione si può esprimere con una formula matematica diciamo che la funzione y = f(x)

è una funzione matematica e la formula che permette di passare dal valore di x al valore di y si dice equazione della funzione.

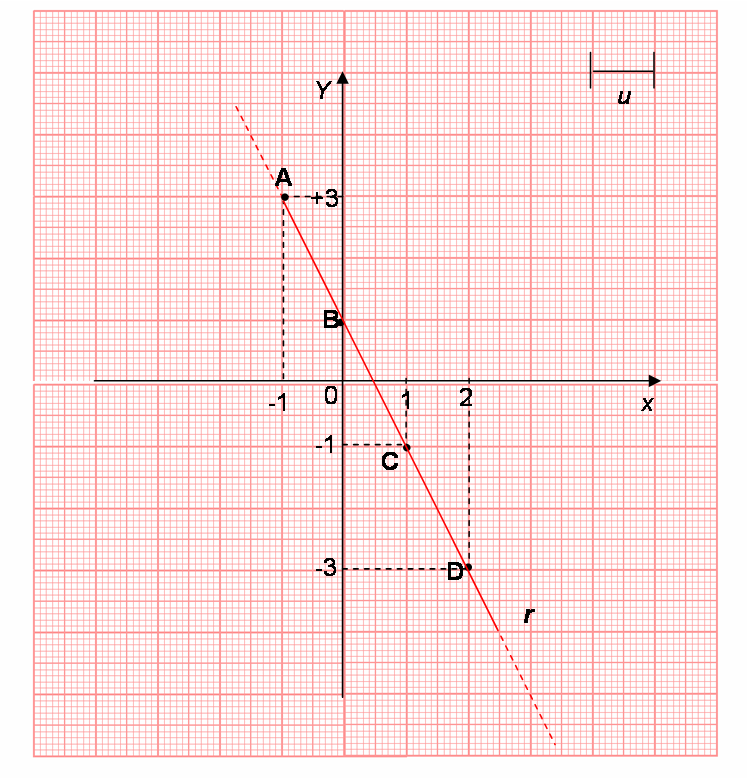
Consideriamo la funzione y = -  2x + 1

Completiamo la tabella dei valori assegnando un valore arbitrario ad x e calcolando il corrispondente valore di y.

Rappresentiamo i punti A(- 1; + 3), B (0; + 1), C(+1; - 1), D(+ 2; - 3) sul piano cartesiano. Unendo questi punti ci accorgiamo che appartengono tutti alla stessa retta r.

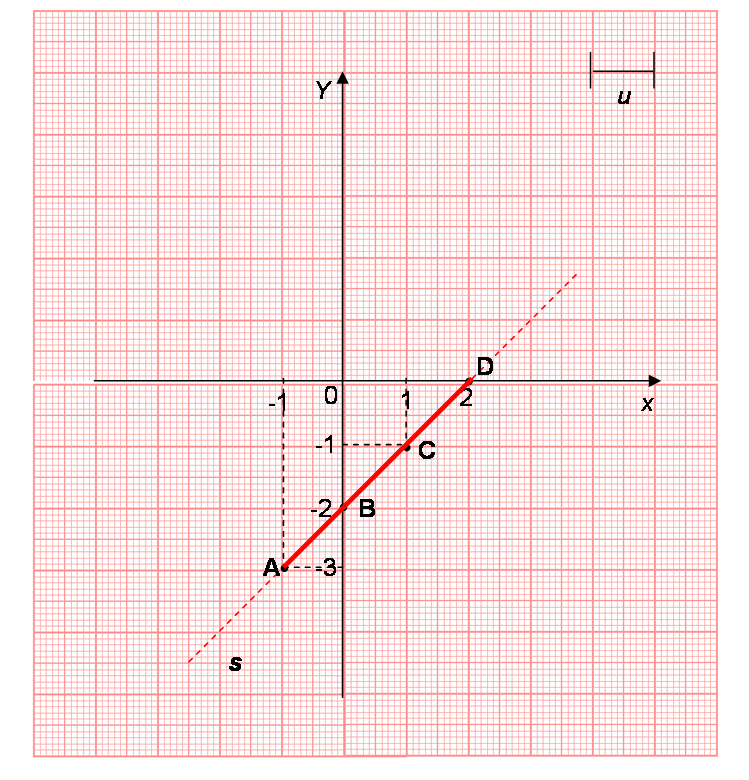
Consideriamo ora quest’altra funzione y = x - 2

Completiamo la tabella dei valori assegnando un valore arbitrario ad x e calcolando il corrispondente valore di y.

Rappresentiamo i punti A(- 1; - 3), B (0; - 2), C(+1; - 1), D(+ 2; 0) sul piano cartesiano. Unendo questi punti ci accorgiamo che appartengono tutti alla stessa retta s.

Osservando i grafici ci accorgiamo  che i termini noti +1 e -2 rappresentano l’ordinata del punto in cui la retta incontra l’asse y.

Possiamo anche notare come equazioni del tipo y = -  2x + 1 o y = x – 2 abbiano come equazione una retta. Possiamo generalizzare dicendo che ogni equazione del tipo y = mx + p (con m e p che indicano qualsiasi numero relativo) ha come equazione una retta.

Per rappresentare nel piano cartesiano una retta ci servono solo due coppie di valori corrispondenti perché per due punti passa una e una sola retta. Vediamo, ad esempio di rappresentare nel piano cartesiano la retta di equazione 

Rappresentiamo la retta di equazione 

ESERCIZI

·      Costruisci la tabella dei valori e disegna le rette rappresentate dalle seguenti equazioni

y = - 4x – 2

y = 1/2x + 2

·      Individua graficamente il punto di intersezione P di ogni coppia di rette r ed s e determinane le coordinate.

r          y = 2x + 7                   s          y = - 4/3x – 3

r          y = - x + 4                   s          y = x